[개발]점이 사각형 안에 있는지 판단하기

 좌표 공간에 사각형을 그리고 점(Point)가 사각형의 내부에 있는지 외부에 있는지 판단하는 로직을 만들고자 하였다.

 

<canvas> 태그 안에 구현

 기존 회사에 있던 로직은 타겟 포인트의 x,y좌표가 사각형의 4개 꼭지점의 x,y좌표 사이에 있으면  사각형 안에 점이 있다고 판단하였다. 이 로직이 제대로 동작하려면 축과 평행한 직각사각형이어야만 한다. 하지만 실제로 사용자가 그리는 사각형은 축과 평행하지 않을 수 있고 찌그러진 사각형일 수도 있다.

다시 고등 수학, 길벗 출판사

이 문제의 해결 방법은 다시 고등 수학이라는 책을 통해 알 수 있었다. 고등학교 시절 수학을 멀리하였으나 개발자가 되고 나서 논리력을 기른다는 관점에서 수학의 필요를 느꼈다. 그래서 중,고등학교 수학 교재와 함께 구매하여 틈틈이 보던 책이 이 책인데 명제부터 시작해서 삼각비나 벡터 같은 개념을 이해하기 쉽게 설명해주는 좋은 책이다.

'벡터의 개념을 이용하면 사각형 안에 점이 있는지 확인 할 수 있지 않을까' 라는 생각에 벡터 챕터를 반복하여 읽어보았다. 그 중 '벡터의 분해'를 이용하면 될 것이라는 생각이 들었다. 사각형의 각 꼭지점을 원점으로 삼고 벡터P를 원점에 인접한 두 꼭지점으로 표현되는 벡터의 합으로 구하는 것이다. 

벡터P = s벡터A + t벡터B

s또는 t가 음수라면, 벡터A 또는 벡터B의 역벡터가 더해진 것이므로 범위 바깥에 있다고 생각하는 것이다.

사각형ABCD와 점P가 있다.

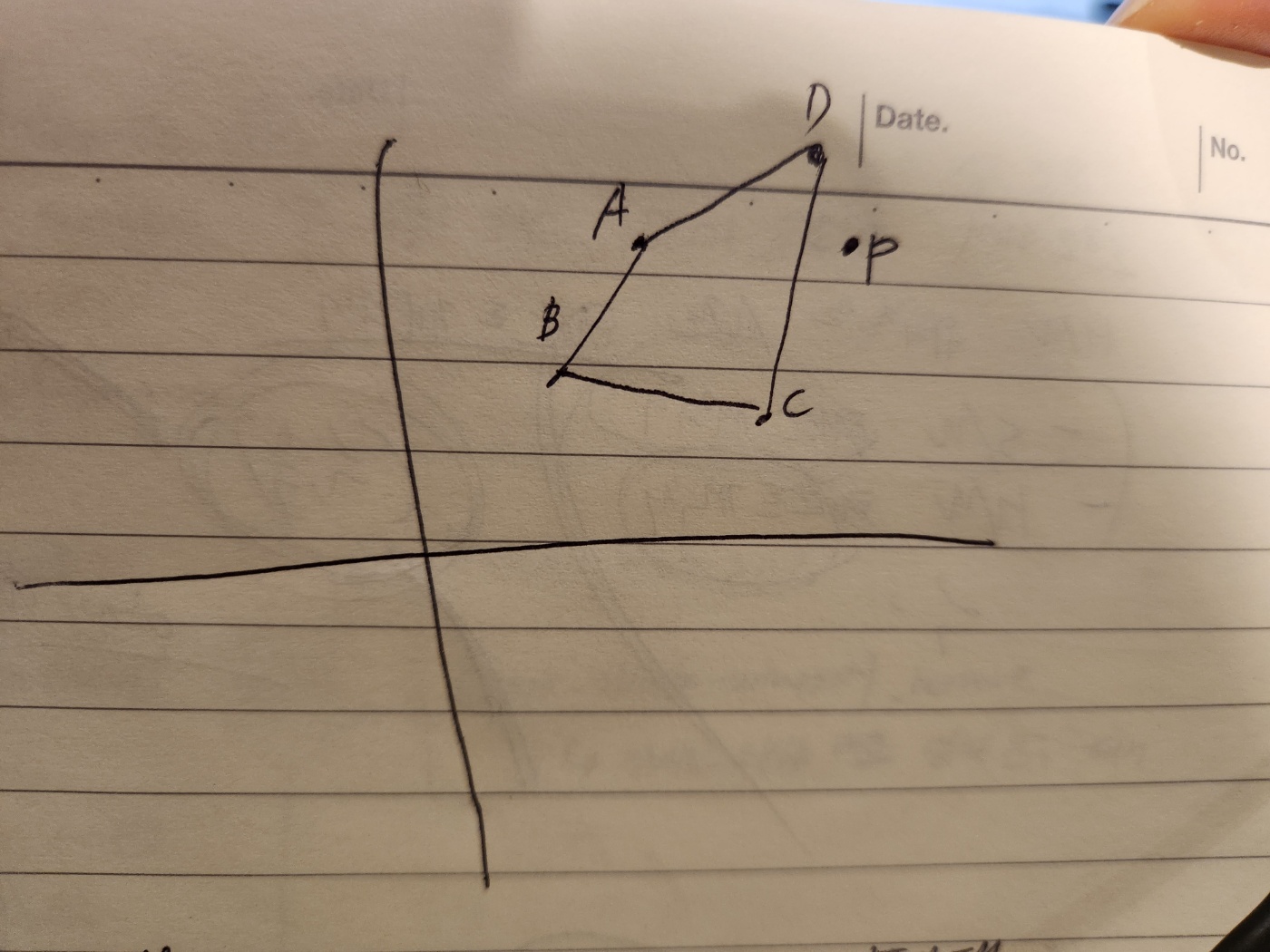
각 꼭지점을 순회하면서 기준 꼭지점을 원점(0,0)으로 보정한다. (인접 꼭지점과 P도 그만큼 평행이동)

A기준일 때 벡터P는 두 벡터의 합으로 표현이 가능

 

B기준일 때 벡터P는 두 벡터의 합으로 표현 가능

D기준일 때 벡터P는 -t벡터A + s벡터C 처럼 성분에 역벡터가 포함된다.

C 기준일 때 벡터P는 -t벡터B + s벡터D 처럼 성분에 역벡터가 포함된다.

 

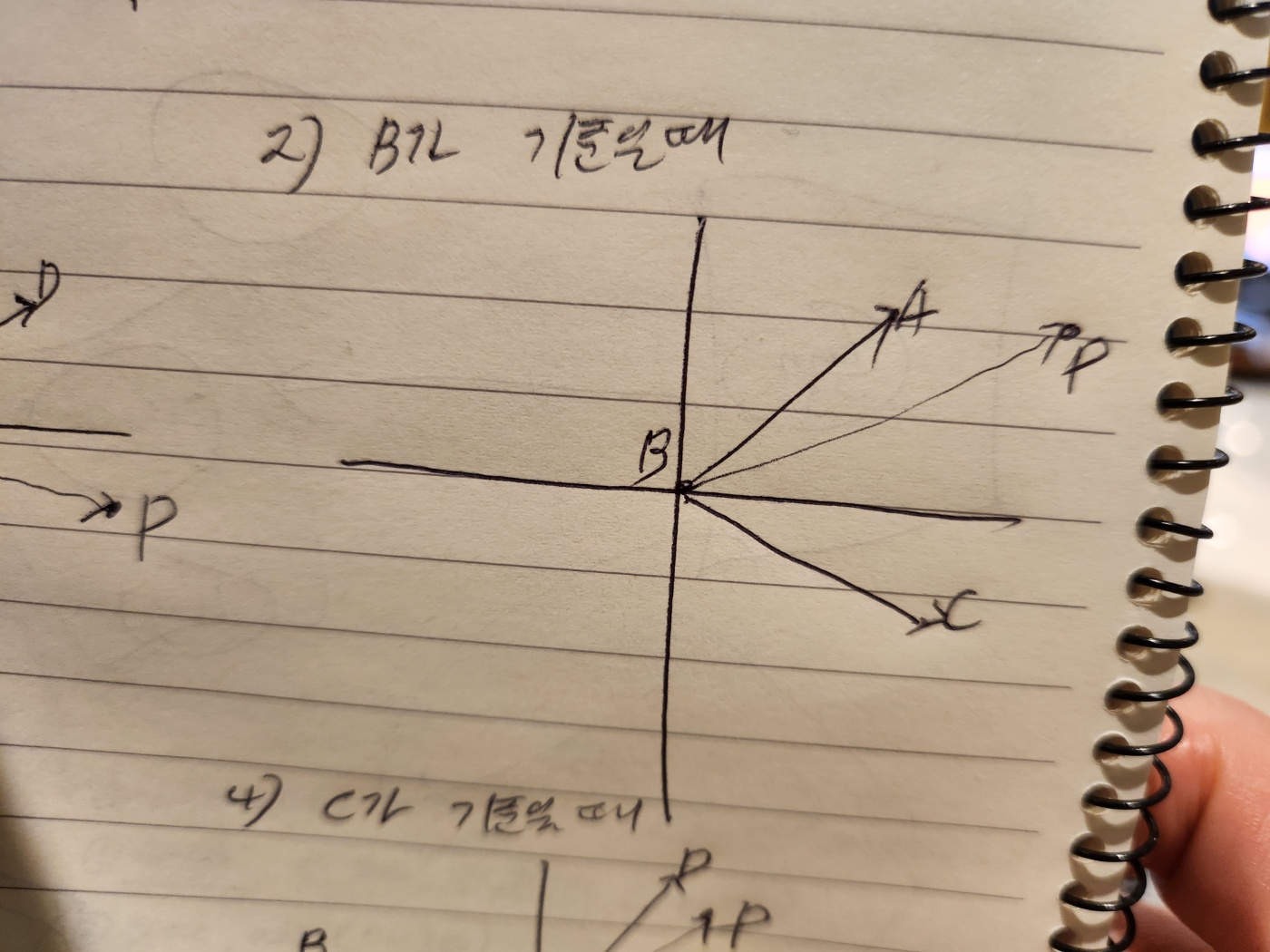
4개의 꼭지점을 기준으로 모든 케이스가 역벡터가 아닌 벡터의 합으로 표현된다면 그 점 P는 사각형 내부에 있는 것이다.

계산은 벡터의 성분표기법으로 간단한 연립 일차방정식이 된다.

연립 1차방정식의 해를 구하는 소스코드

이렇게 계산할 때 1개의 점(Point)가 사각형 내부에 있는지 판단하는 시간 복잡도는 O(1)이 될 것으로 보인다. 단, 해당 로직에도 한계가 있는데 사각형의 내각이 180도 이상이면 안된다. 

---------

좌표가 사각형 안에 있는지 판단하기

1. 좌표에 사각형의 4개 꼭지점을 클릭한다.
2. 사각형의 내부/외부를 클릭하여 좌표가 사각형의 안에 있는지 판단한다.

구현 로직

1. 클릭한 좌표 지점을 T라 한다.
2. 사각형의 각 꼭지점마다 순회한다
   1)기준 꼭지점의 인접 꼭지점을 각각 A, B라 한다.
   2)기준 꼭지점을 원점으로 간주하여 A,B,T의 좌표를 보정한다.
   3)벡터T를 벡터A와 벡터B의 합으로 표현한다.
   4)vec{T} = t * vec{A} + s * vec{B}
   5)t와 s를 구한다.
   6)t 또는 s가 음수이면 false를 반환한다.
3. 사각형의 4개의 꼭지점을 모두 확인하면 true를 반환한다.

 

[깃허브]

playfulcode/canvas-ex at master · mbk1991/playfulcode